丂丂丂丂倵侾倖乮倶侾乯亄倵俀倖乮倶俀乯亄丒丒丒丒丒亄倵値倖乮倶値乯
偙偙偵暘揰倶倝偼俴倕倗倕値倓倰倕偺懡崁幃俹倝乮倶乯亖侽偺崻偱偁傞丅丂
丂丂俹侾乮倶乯亖倶丆丂俹俀乮倶乯亖乮俁倶俀亅侾乯乛俀丆丂俹俁乮倶乯亖乮俇倶俁亅俁倶乯乛俀丆丒丒丒丒丒丅
俴倕倗倕値倓倰倕偺懡崁幃偼師偺慟壔幃偐傜媮傔傞偙偲偑偱偒傞丅
丂丂乮値亄侾乯俹値亄侾乮倶乯亖乮俀値亄侾乯倶俹値乮倶乯亅値俹値亅侾乮倶乯
乕侾偐傜侾傑偱佺俹値乮倶乯丒俹倣乮倶乯倓倶亖2乛(2値+1)丂丂丂値亖倣偺偲偒
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖0丂丂丂丂丂丂丂丂丂値亗倣丂丂丂 丂捈岎宯偱偁傞丅
傑偨廳傒倵倝偼丂俹値乮倶乯乛乮倶亅倶倝乯傪亅侾偐傜侾傑偱愊暘偟偨傕偺傪俹乫値乮倶倝乯偱妱偭偨傕偺偱偁傞丅
埲忋偺偙偲偼倖乮倶乯偺俴倕倗倕値倓倰倕揥奐偵傛偭偰摼傜傟傞丅
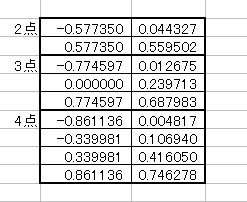 倶倝偲倵倝偺悢抣偵偮偄偰偼乽婎慴悢妛墘廗乿乮嫟棫弌斉乯偵値亖俀丆俁丆係丆俆丆俇
倶倝偲倵倝偺悢抣偵偮偄偰偼乽婎慴悢妛墘廗乿乮嫟棫弌斉乯偵値亖俀丆俁丆係丆俆丆俇偵偮偄偰婰偟偰偁傞偺偱嶲徠偺偙偲丅
丂倎 偐傜 倐 傑偱偺愊暘偺応崌偼
丂丂丂丂倲亖乮乮倐亅倎乯倶亄乮倐亄倎乯乯乛俀
偲曄悢曄姺偟偰忋婰傪揔梡偡傟偽傛偄丅