関数とグラフ(2)
学習内容
- 三角関数・逆三角関数の性質を理解しグラフを描く。
- 指数関数・対数関数の性質を理解しグラフを描く。
Excel の関数 角度の単位はラジアンで
RADIANS,DEGREES・・・ラジアンと角度の単位変換
SIN,COS,TAN・・・三角関数 使用法
ASIN,ACOS,ATAN・・・逆三角関数 使用法
LN・・・自然対数
LOG10・・・常用対数
LOG・・・一般の対数関数 使用法
EXP・・・底がeの指数関数
POWER・・・一般の指数関数 使用法

代数関数以外の関数は超越関数といわれるがその代表的なものが三角・逆三角関数と指数・対数関数である。三角関数が定義される単位円とは半径1の円のことで,その円周上の点P(x,y)と原点を結ぶ 直線がX軸となす角をθ とする。
r を動径,θ を偏角といい,三角関数を次のように定義する。
cosθ=x sinθ=y tanθ=y/x
cos2θ+sin2θ=1
tanθ=sinθ/cosθ θがπ/2 の奇数倍のときはtanθは存在しない
例題1 y=cosx,y=sinxおよびそれらの逆関数y=cos−1x,y=sin−1xの曲線を描け。
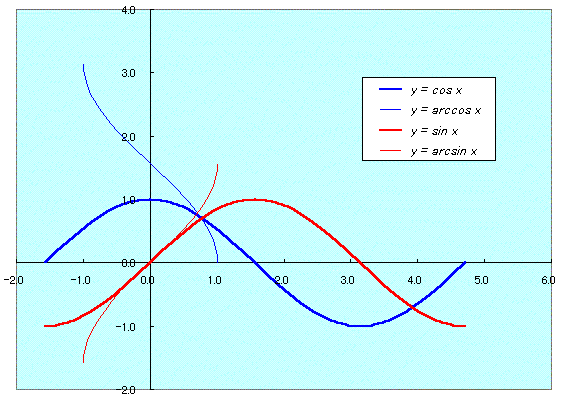
cos は sin を −π/2 ほど平行移動したものである。またy=cos−1x は
0〜πの部分,y=sin−1xは−π/2〜π/2 の部分だけ(主値)が表示されている。
例題2 y=sinx,y=sin2x,y=sin4xのグラフを描き
どのように変化しているか調べよ。

波長が1/2,1/4になっている。すなわちx方向に1/2,1/4倍に縮小されたものである。
例題3 aをx回かけたものをaxと書き表す。xが負数,分数,さらに無理数でも定義可能である。
y=axおよびその逆関数y=logaxのグラフを描け。
0<a<1のとき ,
a>1のとき

対数関数はx>0の時のみ定義できる。
問題1 次の式の値を求めよ。1) sin45°
2) tan135° 3) cos(π/6) 4) sin10.5
5) sin-10.5 6)
tan-11 7) cos-10.3 8) cos-15
9) e+e2 10) 3.53.5 11) log232
12) log(1/100)
問題2 次の曲線を描け。
1) y=cosx+cos2x
2) y=xsinx
3) y=sinx,y=cosx,y=sinx+cosx
を同一座標軸に描け。
4) y=x+logx (自然対数)
5) y= logx2とy=2logxとの違いを表せ。




